数ヶ月前のことですが、業務中に「社会に出て初めて三角関数を使った」という声を聞きました。とあるゲームプログラミング書籍のコードを書いていた社員の発言です。プログラミングをしていると、数学の関数を使う機会は少なくありません。
プログラミング言語にはたいてい数学用のライブラリが用意されていて、例えばPythonならmathという標準モジュールを使えば、次のようにして三角関数の値が求められます。
import math
y = math.sin(math.pi/4)この例では、yには\(\sin \frac{\pi}{4}\)の値である0.707106781…(=\(\sqrt{2}/2\))が代入されます。もちろんどんな数値を入れても(保証される精度の範囲内で)正確な値が得られます。しかし、素朴な疑問として、こういった関数の値がどのように得られるか気になったことはありませんか?
実は、その計算にはテイラー展開という数学の公式が利用されています(利用しないライブラリもあります)。これは関数を別の形に書き換えて、近似するための公式です。
今回の記事では、タイトルにもあるように「近似計算」と「信号解析」について紹介します。しかし、長くなってしまうので3つの記事に分けることにしました。どのように話が繋がっていくのかは、次回の記事をお待ちください。
テイラー展開
テイラー展開は、「どんな関数も\(x\)の多項式で書くことができる」という考え方に基づきます。多項式というのは、\(x\)、\(x^2\)、\(x^3\)、\(x^4\)、\(\cdots\)と、\(x\)の累乗に適当な係数\(c_1\)、\(c_2\)、\(c_3\)、\(c_4\)、\(\cdots\)をかけて足し合わせたものです。数式で書くと次のようになります。
$$c_0 + c_1 x + c_2 x^2 + c_3 x^3 + c_4 x^4 + \cdots$$
このような多項式を\(x\)の関数とみなしてグラフに描くと、グネグネとした曲線になります。
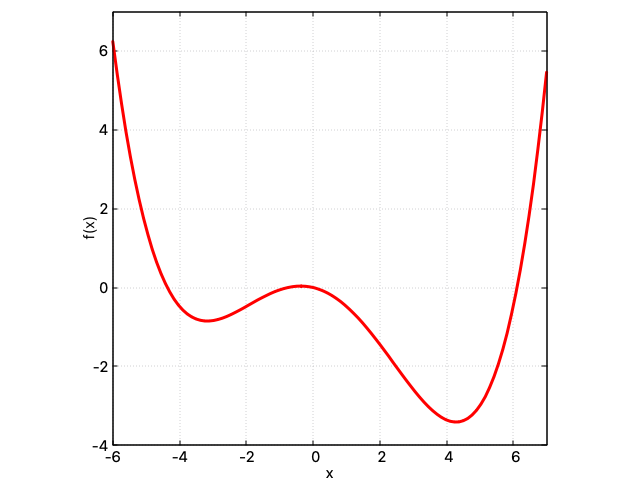
これは\(y=\frac{1}{100}x^4-\frac{1}{100}x^3-\frac{7}{25}x^2-\frac{1}{5}x+\frac{12}{25}\)という数式のグラフで、\(\frac{1}{100}\)、\(-\frac{1}{100}\)、\(-\frac{7}{25}\)、\(-\frac{1}{5}\)、\(\frac{12}{25}\)が\(x\)の係数です。このような係数をさまざまに変えると、それに応じてグラフの形もグニャッと変わるわけです。逆に言えば、この\(x\)の係数をうまいこと調整すれば、\(\sin\)だろうが\(\cos\)だろうが、\(x\)の多項式でいい感じに表現できるのでは? というのがテイラー展開の考え方です。
ところで、先ほどサラッと「この多項式を\(x\)の関数とみなして」と書きましたが、関数というのは変数\(x\)に応じて値が変化する式のことだと思ってください。数学では、\(f\)が\(x\)の関数であるということを\(f(x)\)と書きます。例えば二次関数であれば、\(f(x)=x^2\)と書きますし、三角関数であれば\(f(x)=\sin x\)と書きます。
さて、ようやく本題のテイラー展開です。テイラー展開は、関数\(f(x)\)を次のように表現します。
$$f(x) = \sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n$$
数式に馴染みのない方には意味不明な記号のかたまりにしか見えないと思いますが、記号の意味を理解する必要はありません。最終的にどういう多項式になるのかというところまで眺めてもらえればと思います。
話を単純にするために\(a=0\)として、この式をもう少し平たく書くと次のようになります。
$$f(x)=f(0)+\frac{f^{(1)}(0)}{1!}x+\frac{f^{(2)}(0)}{2!}x^2+\frac{f^{(3)}(0)}{3!}x^3+\cdots$$
まだ意味不明な記号が残っているように見えるかもしれませんが、大事なことは、この式がxの多項式であり、xの係数が決められたルールに従って計算できるということです。さきほど書いた「\(x\)の係数をうまいこと調整すれば」の「うまいこと」が具体的な数式で書かれているのです。
※\(f^{(n)}(0)\)は、\(f(x)\)を\(n\)回微分した関数に\(x=0\)を代入した値という意味
※\(n!\)は\(n\)の階乗(\(n!=n\times(n-1)\times(n-2)\times\cdots\times2\times1\))。例えば\(3!=3\times2\times1=6\)
実際に\(\sin x\)の計算をしてみる
\(f(x)=\sin x\)として実際に計算してみましょう。テイラー展開の式に\(\sin x\)を当てはめると、次のようになります。
\begin{align}f(x) &=\sum_{n=0}^{\infty}\frac{(-1)^n x^{2n+1}}{(2n+1)!}\ \\ &=x – \frac{x^3}{3!} + \frac{x^5}{5!} – \frac{x^7}{7!}+\cdots\end{align}
1行目はごちゃっとしてますが、2行目のように書くと単純な式であることがわかると思います。3、5、7と続けて無限に足してゆけば精度は良くなりますが、身の回りにあるようなコンピュータで計算できる桁数は限られているので、その範囲で足せればプログラミング的には十分です。
この式をプログラムとして実装するのはとても簡単です。実際にPythonのプログラムとして作成して、テイラー展開の部分を抜き出したのが次のソースコードです(NumPyとmathを使用しています)。
def function(x, n):
array = np.empty(0)
for x in x_a:
sum = 0
for i in range(0, n):
sum += np.power(-1, i)*np.power(x, 2*i+1)/math.factorial(2*i+1)
array = np.append(array, sum)
return arrayこのように実装した近似関数を使って、グラフを作成してみました。下の図はPlotlyというライブラリを使って、NumPyの\(\sin\)関数と比較した様子です。緑がNumPyで計算した\(\sin\)関数のグラフ、赤がテイラー展開で近似した\(\sin\)関数のグラフです。グラフの下部にスライダーがあり、スライダーの位置に応じて多項式の何項目まで足すかを変えることができます。実際に動かして確認してみてください。
計算精度を詳しく知るには、正しい値と比較して何桁目まで一致しているかを調べなければなりませんが、このグラフの見た目だけで判断すれば、6項目まで足し合わせれば1周期分ぐらいは正しそうです。
まとめ
今回は例として\(\sin\)関数を取り上げましたが、他の関数も同じようにして多項式で近似できます。さらに、これを応用すると、数学の世界で重要なネイピア数\(e\)について
$$e = 1 + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \cdots$$
という式や
$$e^{i\pi}+1=0$$
という不思議な式を導くこともできます。気になった方はぜひ調べてみてください。
この記事では、プログラミングで使用する数学関数の計算に、テイラー展開という数式が使用されていることを紹介しました。このような近似計算を使えば、四則演算しかできないコンピュータでも、\(\sin\)や\(\cos\)などの数学関数の値が求められることがお分かりいただけたかと思います。
次回は、別の近似計算の方法として、フーリエ級数展開を紹介します。テイラー展開とは一味違う近似計算ですが、これが現代の生活に欠かせない信号解析の手法につながっていきます。数学に馴染みのない方の中には、数式に抵抗がある方もいるかもしれませんが、なるべく噛み砕いて紹介したいと思いますので、お楽しみにしてください。

