最近、業務中にイラストの曲線の描画方法について触れる機会がありました。ここでいうイラストというのは、当社が手がけるような書籍で使われるイラストや、普段何気なく目にしている企業や製品などのロゴマークのようなものです。そうしたものの多くは、Adobe IllustratorやInkscapeなどといったイラストソフトによって描かれています。
イラストソフトで描ける曲線は滑らかで美しいものですが、実際のところは数学的な数式によって計算されたグラフです。中でもよく使われるのが「ベジェ曲線」と呼ばれるものですが、その具体的な計算方法について気になったので、調べてみました。また、数式によって表せる曲線は、ベジェ曲線以外にもいろいろあります。そこで今回は、ベジェ曲線以外の数式でも描ける曲線や図形なども含めてご紹介したいと思います。
単純な図形を表す数式
多くの方は、小学生の頃から高校生ぐらいまでの間に算数や数学を学んだと思います。その中でもおそらく一番最初に触れる「数式で表せる図形」は直線でしょう。y=ax+bという形で表せて、この関係式を満たすようなxとyの点をグラフ上にプロットしていくと直線になります。
aやbの値を変化させると、直線の傾きが変化したり上下方向に移動したりします。
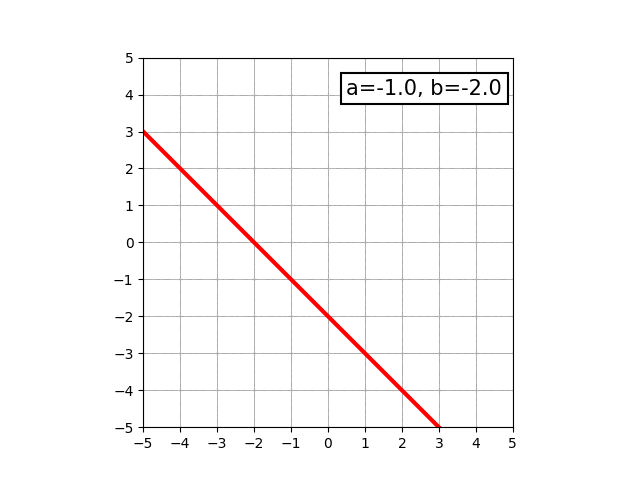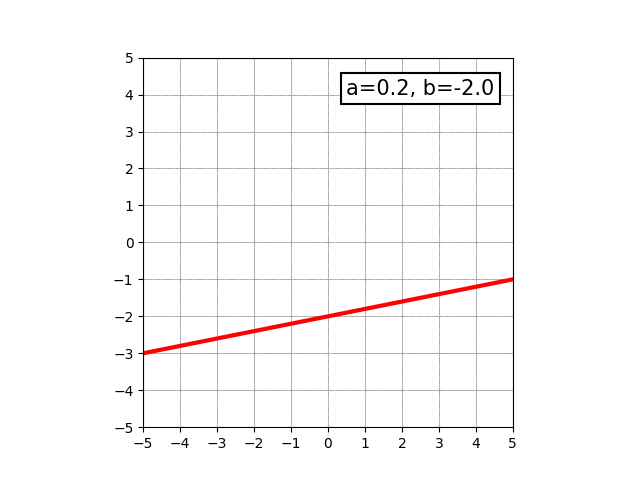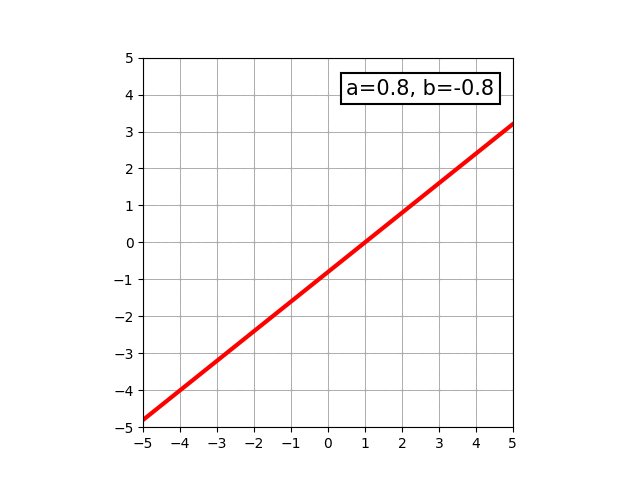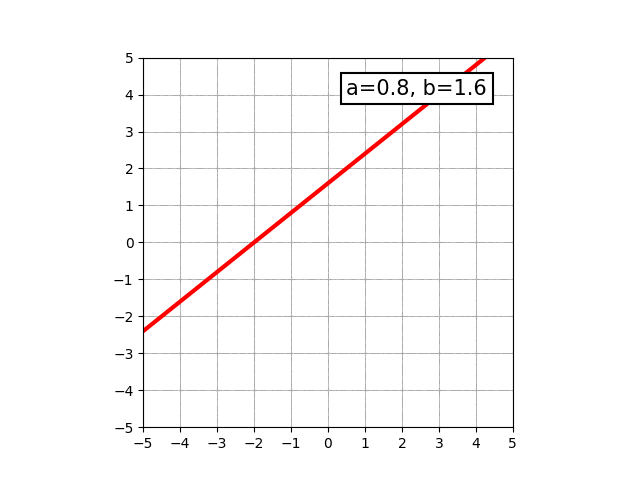
中学生になると、y=ax2+bという形で表せる、いわゆる放物線と呼ばれる曲線を学びます。物を放り投げた時に描く軌跡がこの形になります。aの値によって、開き具合が変わったり開く向きが変わったりします。
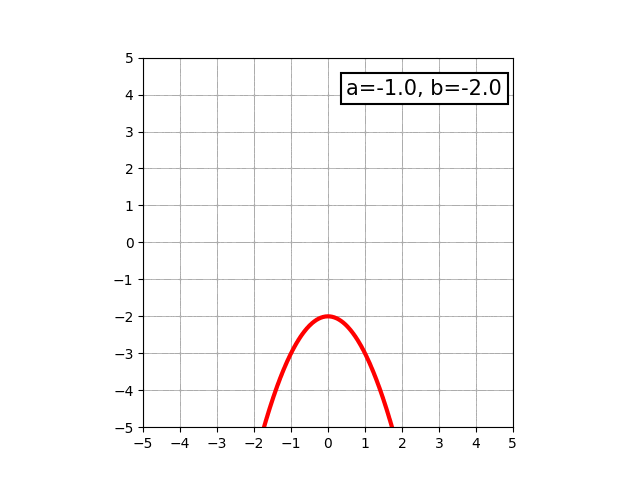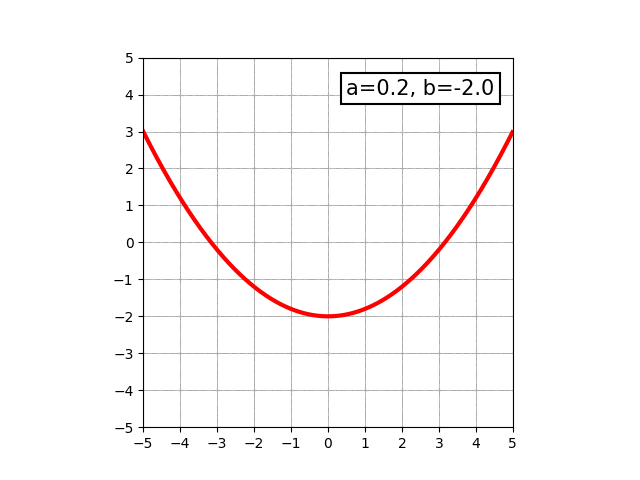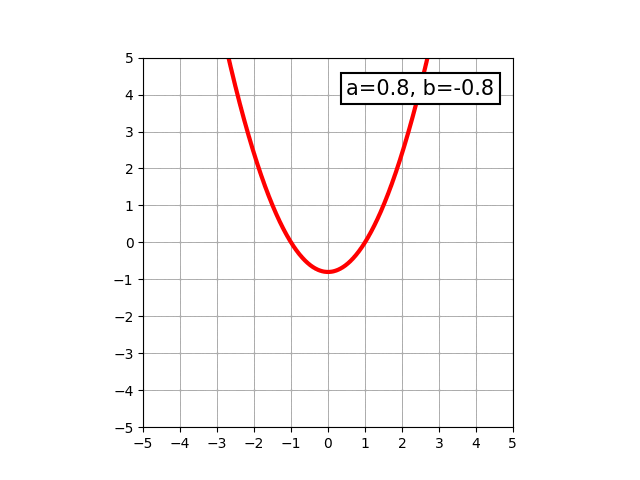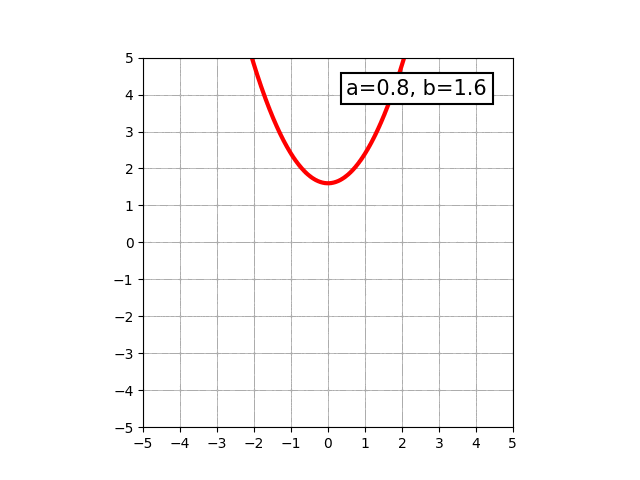
さらに学んでいくと、もう少し複雑な三次関数で表せる曲線や、円などの図形についても学びます。三次関数で表せる図形で最もシンプルなものは、y=ax3という形で表せます。
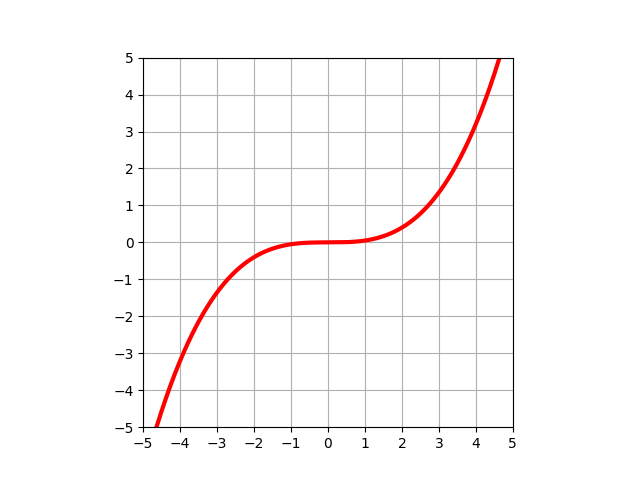
また円はx2+y2=a2と表せます。
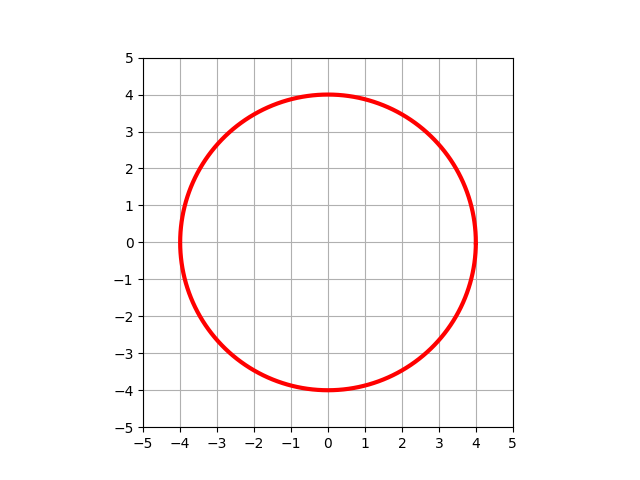
イラストソフトで使われる円の図は、この数式を使っているわけですね。
数学の関数で表せる図形には他にもさまざまなものがありますが、基本的にはxとyの関係式によって描くことができます。こうした単純な図形だけでも、組み合わせることで面白い絵を描けます。
例として、実際に大学の入試問題として出題されたものをご紹介します。次のような問題(2000年 静岡大学 前期日程、抜粋)です。
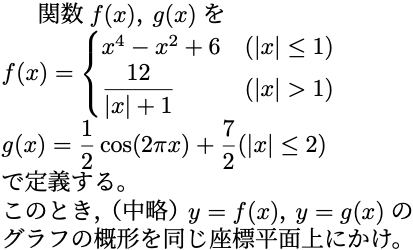
一見するとゴチャッとしていて難しそうに見えますが、高校で学ぶ数学の知識を駆使すると、これらの数式で表される図形を描くことができます。丁寧に解いても良いのですが、今回はそうした労力を一切省いてコンピュータに描いてもらいました。それが下の図です。
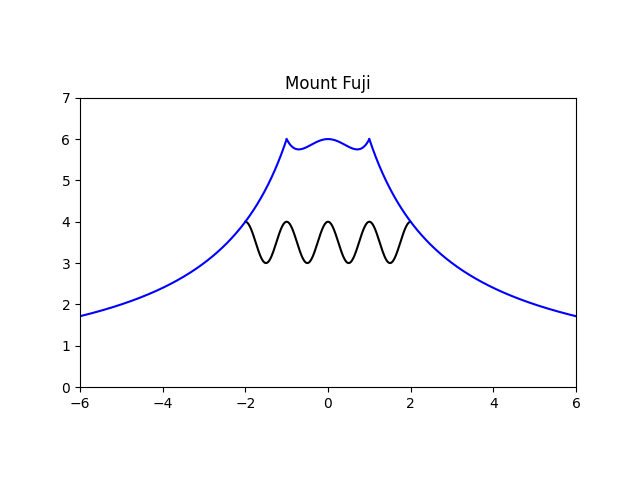
なんと、富士山です。静岡県らしい遊び心あふれた入試問題ですね。
こうした数式によって描かれたグラフを組み合わせて描くイラストを「関数グラフアート」と呼び、コンテストも開催されているようです。
http://www.ge.fukui-nct.ac.jp/~math/graph_art/
過去の入賞作品を見てみると、シンプルで美しいと感じるものから、「よくこんな絵が描けたな」と思うほど複雑なものまでさまざまです。一口に関数グラフアートといっても、描く人の個性がよく現れていて、眺めているだけでも楽しいですね。
パラメータ表示
さて、ここまで見てきた図形は、xとyを=(イコール)によって結びつける関係式によって表現できる図形ばかりでした。しかし、世の中にはそう単純には表現できない図形もたくさんあります。
身近な例としては、スピログラフが挙げられます。耳慣れない単語かもしれませんが、子供の頃にこんな模様が描ける道具で遊んだ経験はないでしょうか。

下の写真のような、歯車のような部品の穴にペンを挿し、それとセットの定規についている穴の中でグルグルと回して描いたアレです。

下のアニメーションはその「グルグルと回して模様を描く様子」を示しています。
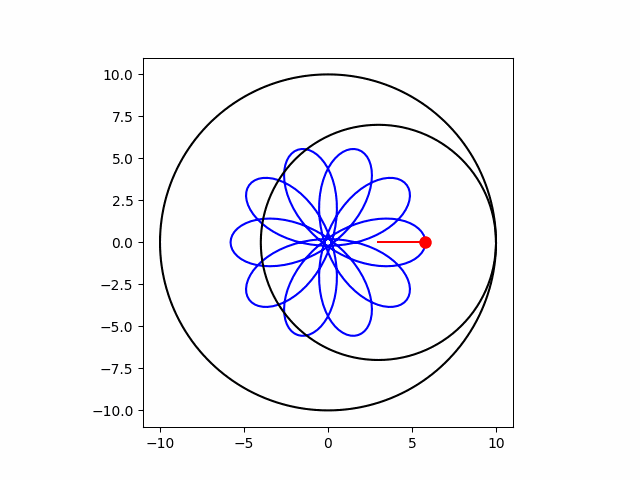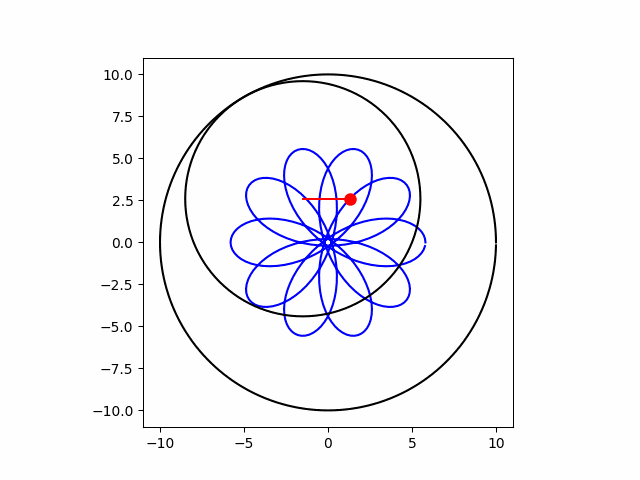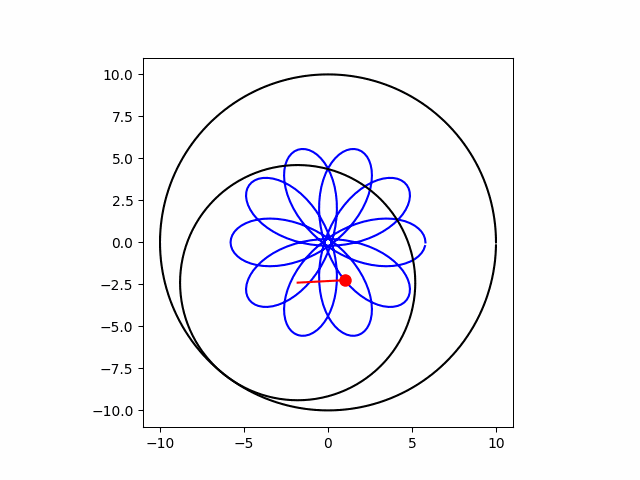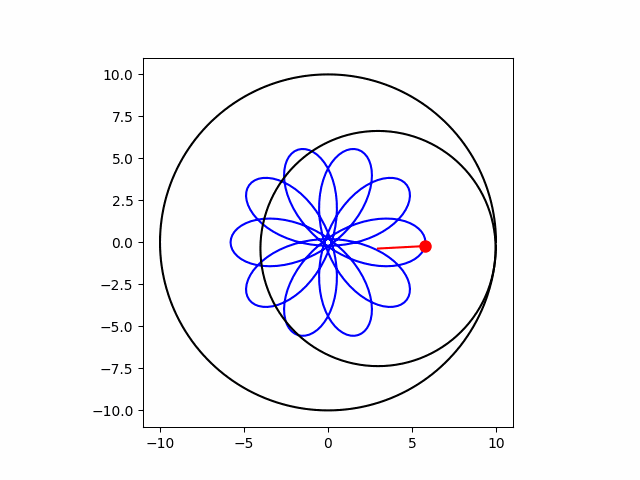
この一見複雑な模様ですが、実は次のような単純な数式で表現することができます。
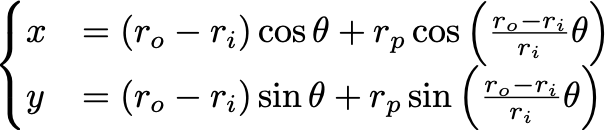
この数式の中にあるroとriはそれぞれ外側の円とその内側を回転する円の半径です。そして、rpはペンを挿す穴と回る円の中心の距離です。θは、外側の円の角度θの位置に回転する円があることを意味しています。図にすると、下のような関係になります。

さて、ここでポイントとなるのが、この図形を表す数式が、これまでと違ってxとyが=(イコール)で繋がっていない点です。その代わり、共通してθ(シータ)という変数を媒介して表現されています。このような表現方法を「パラメータ表示」や「媒介変数表示」などと呼びます。
さきほど表示したスピログラフのアニメーションは、私が作成したプログラムで出力したものですが、こちら(https://nathanfriend.io/inspiral-web/)のサイトに行けば、Webブラウザ上で簡単にスピログラフを描くこともできます。穴の位置や円の大きさなどを自分で設定し、マウスでグルグルするだけです。
もう1つ、パラメータ表示で描ける面白い図形を紹介します。Wolfram alphaのページ(https://www.wolframalpha.com/)を開き、「ダースベイダー」と検索してみてください。すると、次のような結果が表示されます。
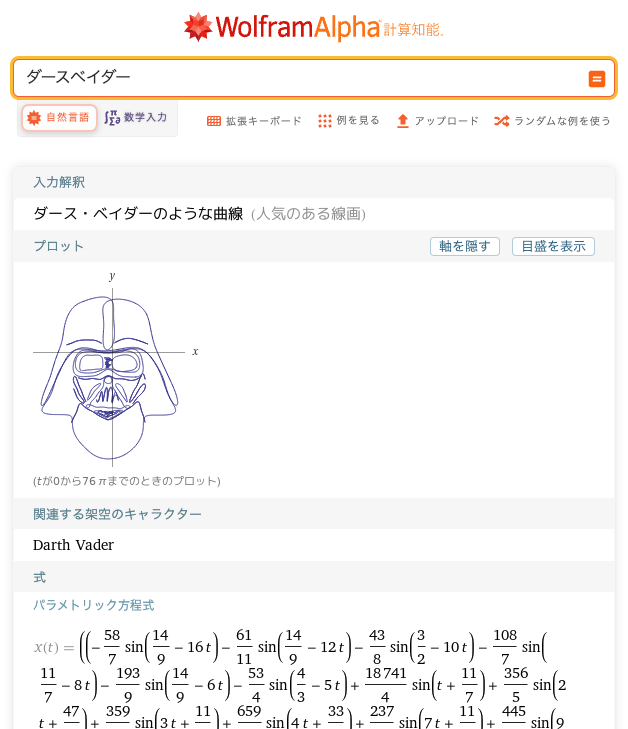
あの見覚えのあるフェイスマスクがグラフとして表示されています。そして、グラフの下には、xとyがtを媒介変数とする数式でそれぞれ表示されています。思わず笑ってしまうほど長い数式なのですが、いかに長い数式かは、ぜひご自身で検索して確かめてみてください。
それにしても、どのようにして導き出したのかは不明ですが、こんなグラフが作れてしまうのは面白いですね。
ベジェ曲線
さて、前置きがだいぶ長くなりましたが、やっと本題です。イラストソフトの曲線描画機能で使用されている数式の多くは、ベジェ曲線と呼ばれるものです。ベジェ曲線は、次のような数式で表すことができます。
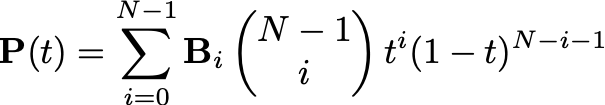
いままで見てきた数式と全然雰囲気が違いますね。でも実はそんなに難しい式ではありません。もう少し見通しをよくするために、具体的に考えてみます。
ここでポイントとなるのが、Biという記号で書かれた「制御点」と呼ばれるもので、これが曲線の形を決めています。ここではB0からB3までの4個の制御点をグラフ上に用意することにし、制御点Bnのx, y座標をxnやynと書くことにします。また、数式中のかっこ(N-1とiが縦に並んでいる)は二項係数と呼ばれるもので、詳しいことは省略しますが、簡単に計算できます。
すると、上の式を先程までの見慣れた形に書き直すことができ、次のようになります。
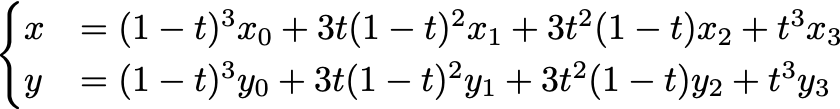
これは先ほど見たのと同じ、tを媒介変数とするパラメータ表示ですね。
制御点の座標を試しにB0=(0,0)、B1=(0.5, 1)、B2=(3,3)、B3=(4,0)とおいてプログラムに計算させ、グラフに表示してみました。
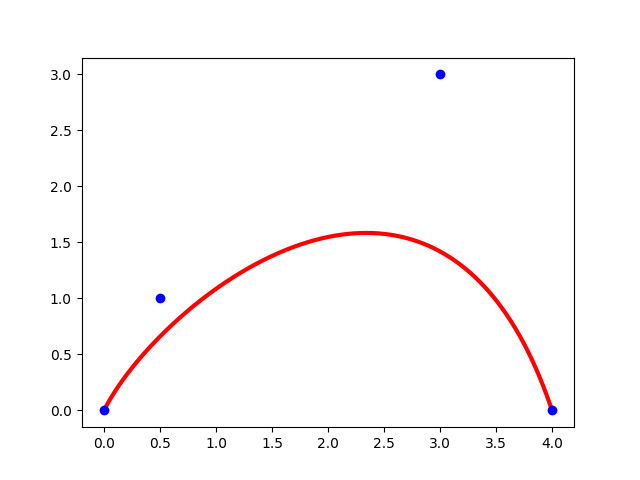
制御点が青い4つの点、それらの座標を使って計算して出てきたベジェ曲線が赤い線です。
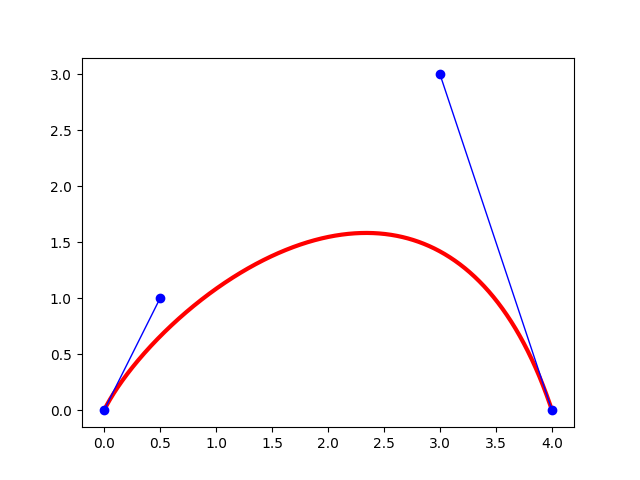
イラストソフトでベジェ曲線を使用したことがある方はピンときたかもしれませんが、この4つの点はイラストソフト上でユーザーが制御する「アンカーポイント」と「ハンドル」と呼ばれるものに対応します。アンカーポイントは描きたい曲線の両端の点で、ハンドルは曲線をどの方向にどれぐらいの強さで伸ばすかを制御する点です。下の図のように、両端の制御点からその隣の制御点に線を引いたような形でよく見かけます。
今度は今のとは別の制御点を置いて、プログラムでベジェ曲線を描いてみました。そしてイラストソフト(Inkscape)でアンカーポイントとハンドルの先端がその制御点と同じ位置になるように置いて曲線を描き、比較してみました。それが次の図です。
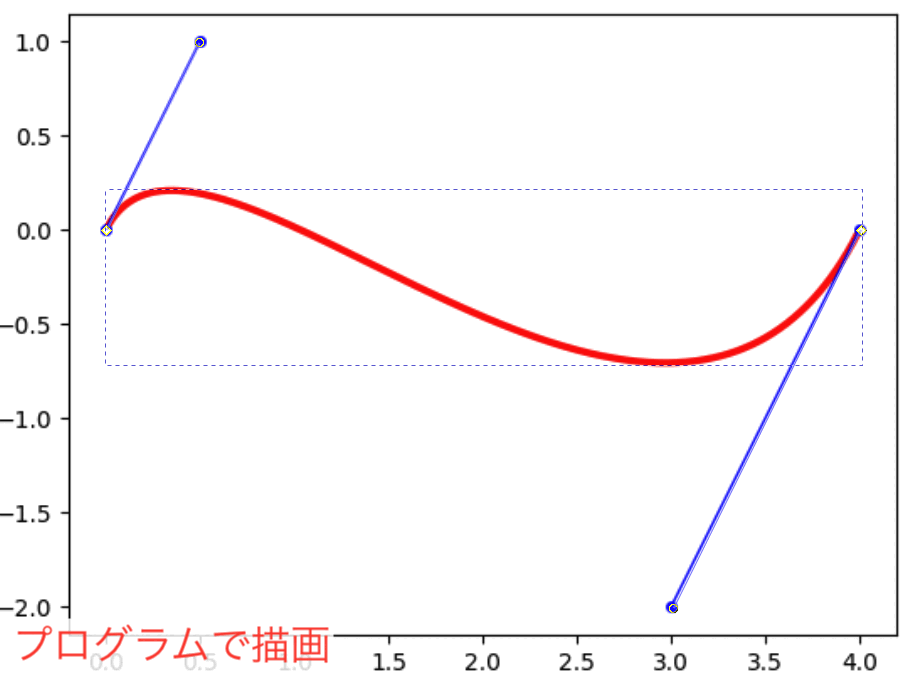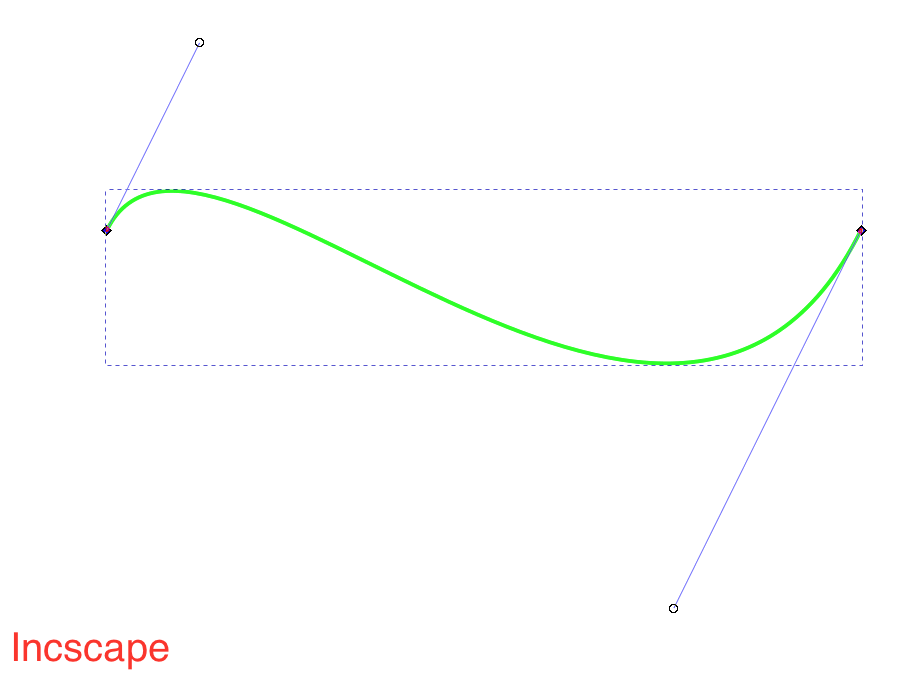
きれいに一致しました。
制御点をどのように置けば描きたい曲線が得られるかというのは、実際に描画しながらでないとなかなかわからないものです。その点、イラストソフトはアンカーポイントやハンドルを直感的に移動でき、リアルタイムに結果を確認できるので、手軽で大変便利です。コンピューターのおかげでこうした面倒な手順を省略できるので、絵描きの方は余計な手間を取らずに本業に集中できるというわけですね。
おわりに
数式によって表現できる図形について、簡単にまとめてみました。直線や円などの基本的な図形が数学的に描けるという認識はあったかもしれませんが、イラストソフトで使われる多くの曲線も、そうした図形と同じように数学的に表せることが改めてお分かりいただけたのではないかと思います。
なお、本記事で描画したグラフを作成したプログラムは、GitHub上に公開しています(https://github.com/TEnomoto-lib/graphs_for_blog)。自分でも試してみたいという方は、参考にしていただければと思います。

