「うちの犬のほうが可愛い」論争に終わりはない
共通の趣味を持つ友人と話をしていて、自分の贔屓にしている人(AKB48登場以降の言い方では「推し」)と、友人の「推し」のどちらが優れているかで言い争いになったことはないだろうか?
サッカーではメッシかロナウドか、アイドルでは聖子か明菜か、経済政策ではケインズかハイエクか、広瀬ではアリスかすずか……。
こういった「推し論争」を繰り広げるのはなにも現代の人びとだけでなく、江戸時代には赤穂浪士の討ち入りによって浅野推しか吉良推しのどちらに理があるか江戸中で議論されたというし、平安貴族たちも『源氏物語』の紫の上推しと六条御息所推しに分かれて言い争っていたに違いない。
「推し」をめぐる争いは時を超え、あらゆる分野で勃発する危険性があるだけに、私などは初対面の人と共通の趣味があるとわかっても、お互いの「推し」が異なる可能性を考えてあまり深くは掘り下げないことがある。
異なる「推し」同士を争わせる場合に一番発生しやすい問題は、「論点が統一されず、泥沼化すること」だ。
たとえば、『ドラゴンボール』という共通の漫画が好きな2人が、孫悟空とベジータというキャラクターをそれぞれ好きだとする。
悟空ファンは彼の強さに惹かれ、作中の大半の時点で悟空のほうがベジータより強いことを強調するかもしれない。それに対してベジータファンは彼の内面の変化に惹かれ、最初は残虐な敵として登場したベジータが時の流れのなかで「夫」や「父」の顔を持つようになったことを強調するかもしれない。
この2人は「強さ」と「内面の変化」というそれぞれ別の論点で相手を言い負かそうとしているため、決着のつけようがない。悟空とベジータを評価する共通の基準が2人のあいだに存在しないため、この争いは泥沼化せざるをえないのだ。
決着をつけるための共通の基準のない争いは、たとえるなら同じフィールドに立ちながら別のスポーツで戦っているようなものだ。1人がバットを持って相手の投げる球を打とうとしているのに対し、もう1人は柔道着を着て相手の襟を掴もうとしているところを想像してほしい。
2人で丁寧に論点を整理したうえで、互いの意見を尊重しあい、終始「悟空と、ベジータと、それから私、みんなちがって、みんないい」の金子みすゞマインドに立ちつづけて議論ができればよいが、そのための時間が取れない場合は初めからお互いの「推し」がわからないまま会話を終えてしまうほうが無難だ。
だが、もし意図せず「推し論争」を勃発させてしまった場合はどうすればいいのか?
今回は、「推し論争」を不毛な殴りあいに発展させず、しかも両者が納得できる決着をつけて終わらせるためのテクニックを紹介しよう。
そのために必要なのは紙とペンと、場合によってはWikipediaだ。
決着のための切り札、六次の隔たり
「六次の隔たり」という言葉をご存知だろうか?
世界中のすべての人は友だちの友だちの……友だちを介して繋がっていて、友だちのネットワークをたどればどんな人からどんな人にでも6ステップ以内で到達できるという仮説だ。
この「六次の隔たり」という概念は、「推し」同士を評価する共通の基準をつくるのに利用できる。その方法を解説する前に、もう少し詳しく「六次の隔たり」について見てみよう。
下にあるのが友だちのネットワークのイメージ図だ。
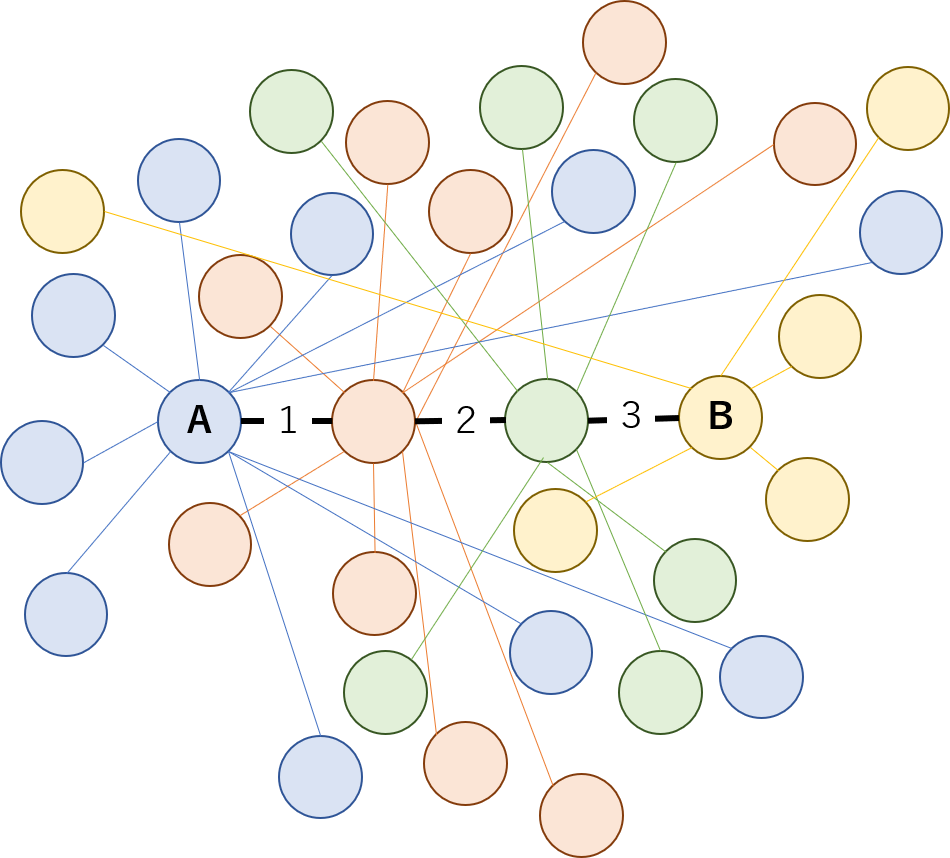
丸が人を表し、線で繋がれた人同士は友だちとすると、AさんとBさんは3ステップで繋がっていて、この図にいるすべての人は5ステップ以内で繋がっていることになる。
「六次の隔たり」仮説では、カムチャツカの若者とメキシコの娘も、ニューヨークの少女とローマの少年も、この記事を読んでいるあなたとこの記事を書いている私も、とにかく世界中の誰と誰を選んでも、その2人は友だちのネットワークを通じて6ステップ以内で繋がっているとされる。
実際、1人あたり(他の人と重複しない)友だちが45人いるとすれば、地球の総人口が「六次の隔たり」以内に収まる計算になる(45の6乗=約83億人)。
ベーコン数を持たずんば俳優にあらず?
ハリウッド映画界には、「六次の繋がり」を利用して俳優の序列を決めるジョークが存在する。
友だちのネットワークではなく共演作による結びつきで、俳優ケヴィン・ベーコンとどれくらいの距離にあるかを示すベーコン数(Bacon number)がそれだ。
ベーコン数の計算方法は簡単だ。ある映画においてケヴィン・ベーコンと共演した俳優には、栄光のベーコン数1が与えられる。そして、ベーコン数1の俳優と共演した俳優にはベーコン数2が与えられ、ベーコン数2の俳優と共演した俳優にはベーコン数3が……と続いていく。
たとえば、ブラッド・ピットは『スリーパーズ』でケヴィン・ベーコンと共演しているため、ベーコン数1を持つ。そして、ベーコン数1のブラッド・ピットと『ファイトクラブ』で共演したエドワード・ノートンはベーコン数2を持つ、といった具合に計算できる。
ベーコン数はもともと、20世紀最大の数学者と呼ばれるポール・エルデシュ(1913-96)と共著論文を介してどれくらいの距離で繋がっているかを示すエルデシュ数(Erdos number)を、俳優の世界に置き換えたものだ。
エルデシュは生涯で1,525もの論文(20世紀の数学者として最多)を執筆し、その共著者は511人にのぼる、まさに「数学界の中心」と呼ぶにふさわしい数学者である。
そのため、世界中のほとんどの数学者が共著論文を介して彼と繋がっているとされ、友人たちがジョークとして「エルデシュ数」を考案し、その値を競うようになったのがエルデシュ数のはじまりだ。
それをハリウッド映画界に置き換えると、ケヴィン・ベーコンになるというわけである。
「ハリウッド映画界の中心」としてケヴィン・ベーコンが選ばれたのは、彼自身が1994年に映画雑誌のインタビューで「ハリウッドで活躍する俳優の全員が、私の共演者か、共演者の共演者だ」と(おそらく冗談まじりに)発言したからとされている。
しかし、その言葉もまったくの虚言というわけではなく、1978年からの長いキャリアがあり、『フットルース』のような青春映画から『ア・フュー・グッド・メン』のような法廷劇まで、さらに『アポロ13』のような実話ベースの映画から『X-MEN ファーストクラス』のようなコミック原作の映画まで、出演してきたジャンルも幅広いケヴィン・ベーコンはまさに「ハリウッド映画界の中心」といっても過言ではない。
実際、ほとんどのハリウッド俳優はベーコン数2以内に収まり、ハリウッドデビューをしていない世界中のあらゆる俳優もベーコン数3に収まるとされる。日本人では渡辺謙、小栗旬、浅野忠信、寺島しのぶなどがベーコン数2を持っているため、彼らと共演した俳優はみなベーコン数3を持つことになる。
解決法その1 「中心」との距離を求める
「推し論争」の話に戻ろう。
あなたが戦わせたい「推し」が数学者か俳優であれば、話は単純だ。ただエルデシュ数、ベーコン数を求めて、相手の「推し」と比べればいい(※1)。
80年代からアクション映画界最大のライバルと目されてきたアーノルド・シュワルツェネッガーとシルヴェスタ・スタローンを例に挙げよう。
シュワルツェネッガーは『コマンドー』でビル・パクストンと共演し、ビル・パクストンは『アポロ13』でケヴィン・ベーコンと共演しているので、ベーコン数は2だ。
スタローンは『パラダイス・アレイ』でトム・ウェイツと共演し、トム・ウェイツはドラマ『クイーンズ・ロジック』でケヴィン・ベーコンと共演しているので、スタローンのベーコン数も2である。
よって、ベーコン数において同点となるため、この2人のあいだに優劣は付けられないことになる(※2)。
戦わせる「推し」が数学者でも俳優でもない場合は、エルデシュ数、ベーコン数に類するものを、以下の3ステップで相手と共同で作ればいい。
- その「推し」が属する分野の中心となる人物を決める
- 中心との距離の測り方を決める
- 実際に距離を求める
たとえば、サッカー選手を戦わせるとしたら①でペレやマラドーナを選び、②で彼らと同じチームに属した経験があったら距離1というルールを決める。そして③で実際に距離を求めるのだ。
①で「中心」に選ぶのは「その分野に詳しい人なら全員が評価する人」で、かつ「その分野に詳しくない人からはあまり知られていない人」が適しているだろう。数学界におけるポール・エルデシュ、映画界におけるケヴィン・ベーコンがまさにそういう存在だからだ。
その意味では、私はサッカーにそれほど明るくないので上の例でペレやマラドーナを挙げたが、ポルトガルのエウゼビオやオランダのヨハン・クライフを「中心」に選んだほうがよいかもしれない。この2人のことは、いま「サッカー 昔 有名人」で検索してはじめて知った。
とはいえ、誰を「中心」に選ぶかで殴りあいの喧嘩になってしまっては「推し論争」を平和に解決するという本来の目的が果たせないため、「中心」について意見が違った場合はお互いに歩み寄ることも重要だ。
解決法その2 どちらがよりよい「中心」かを求める
では、戦わせる「推し」がまさにその分野の「中心」である場合はどうすればよいだろうか?
『ドラゴンボール』の悟空とベジータの例に戻れば、この作品の「中心」はどう考えても主人公である悟空だ。これでは悟空の「中心」との距離はゼロになり、ベジータには勝ち目がない。
このような場合は、膨大な手間がかかることにはなるが以下のようなステップで勝負をつける方法が考えられる。
- 「推し」と同じ分野に属する人物をすべて(1人残らず)リストアップする
- 「推し」との距離の測り方を決め、①で挙げた全員について距離を求める
- すべての人物の「推し」との距離の平均値を求める
つまり、その世界でどれだけよい「中心」であるかを数値で求めるのだ。
そもそも、「六次の繋がり」は世界中の誰を起点に選んでも6ステップ以内で誰にでもたどりつけるという仮説であるため、ネットワークにいるすべての人が等しく「中心」だ! という言い方もできる。
しかし、「みんなが世界の中心だよ!」という平和な結論に飛びついてしまっては永遠に決着をつけられない。論争を終わらせるには、「どちらがよりよい中心か?」まで考える必要があるのだ。
どちらがよりよい「中心」であるかを計算するためには、ネットワークに属するすべての人との距離を測る必要がある。
冒頭でも見た以下の図で、AとBのどちらがよりよい「中心」かを調べてみよう。
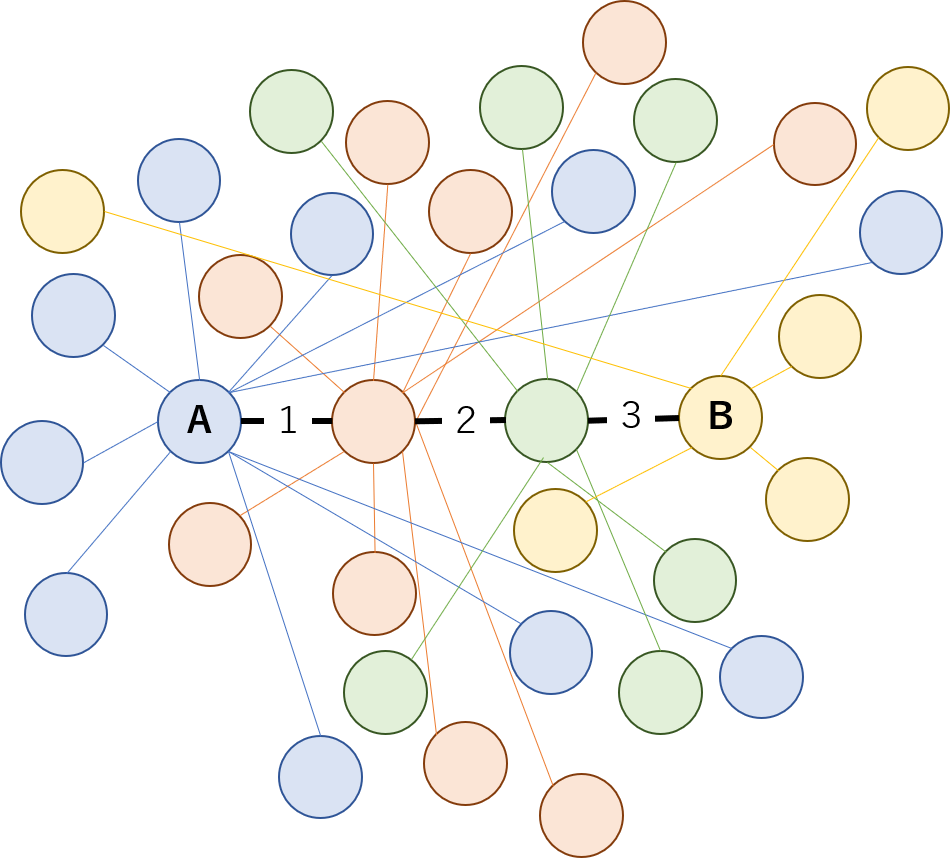
Aと距離1の関係にある人は10人、距離2の人は10人、距離3の人は7人、距離4の人は5人なので、距離の平均は2.21875になる。
同様にBとすべての人の距離の平均を求めると、2.78125になる。
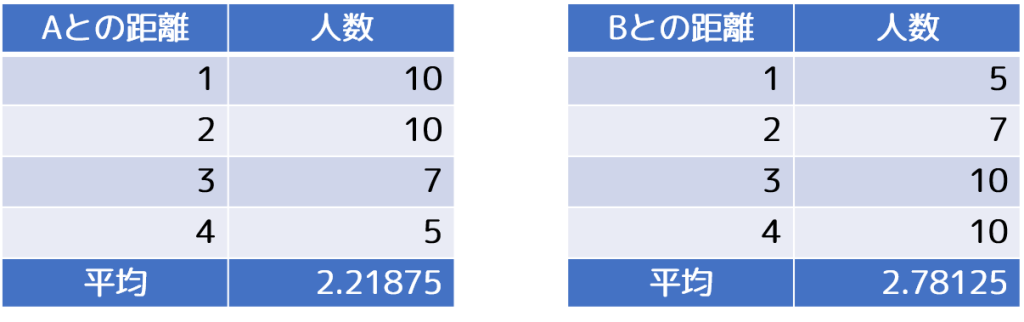
よって、すべての人からの距離が小さいAのほうが、よりよい「中心」であるといえる(※3)。
先ほども書いたが、この方法は膨大な手間がかかるため双方の協力が必須になる。悟空とベジータの例ならば、『ドラゴンボール』に登場する名前のあるすべてのキャラクターをリストアップし、戦ったことのあるキャラ同士は距離1としてすべてのキャラクターについて距離を求めて、さらにその平均を計算し……という作業になる。
「推し」のためならそれだけの手間も厭わないという人は、挑戦してみるといいだろう。私もその結果だけは知りたい。
※1
ベーコン数を求めるためには、ORACLE OF BACONというWebサイトを使うとよい。英語版Wikipediaから情報を抜き出して、任意の俳優とケヴィン・ベーコンの距離を表示してくれるサイトだ。
ベーコン数を求める以外にもさまざまな興味深い使い方ができるので、ぜひ覗いてみてほしい。
https://oracleofbacon.org/
※2
ついでに冒頭で書いた広瀬アリス/すずも、両方がベーコン数3で同点という結果になる。
※3
同じ方法でハリウッド映画界においてケヴィン・ベーコンがどれくらいよい「中心」かを計算すると、594,966人のなかで577番目によい中心であるという結果になるらしい(2022年1月26日閲覧)。
https://oracleofbacon.org/center.php

