前回の振り返り
前回の記事(https://libroworks.co.jp/?p=6287)を投稿してから10ヶ月も経ってしまいました。まずは簡単な振り返りから始めたいと思います。
なお、シリーズ的に3回に分けて投稿する予定でしたが、2・3回目に書くつもりだった内容を今回の記事で1つにまとめ、全2回の記事に短縮いたします。
テイラー展開
前回の記事を一言で表せば「テイラー展開を使えば、どんな関数\(f(x)\)も、\(x\)の多項式で表現できる」というものでした。数式で表すと次のようになります。
$$f(x)=\sum_{n=0}^{\infty}\frac{f^{(a)}(n)}{n!}(x-a)^n=f^{(0)}(a)+f^{(1)}(a)(x-a)+\frac{f^{(2)}(a)}{2!}(x-a)^2+\cdots$$
そしてこの例として、次のように\(y=\sin x\)という波形の関数を\(x\)の多項式で近似したグラフを紹介しました。
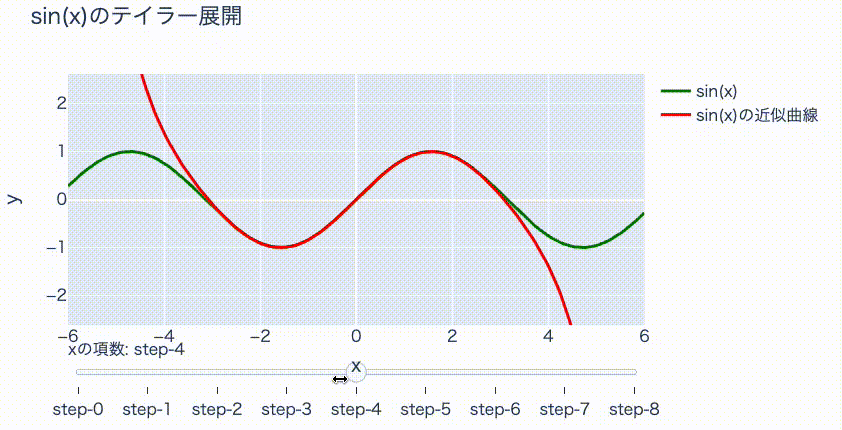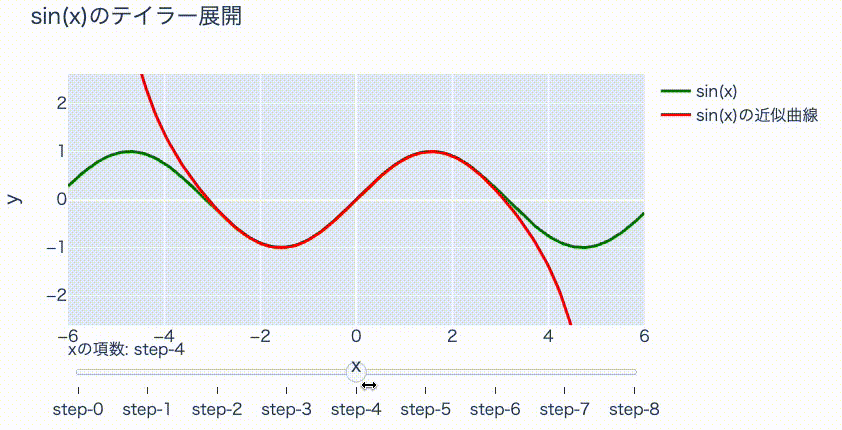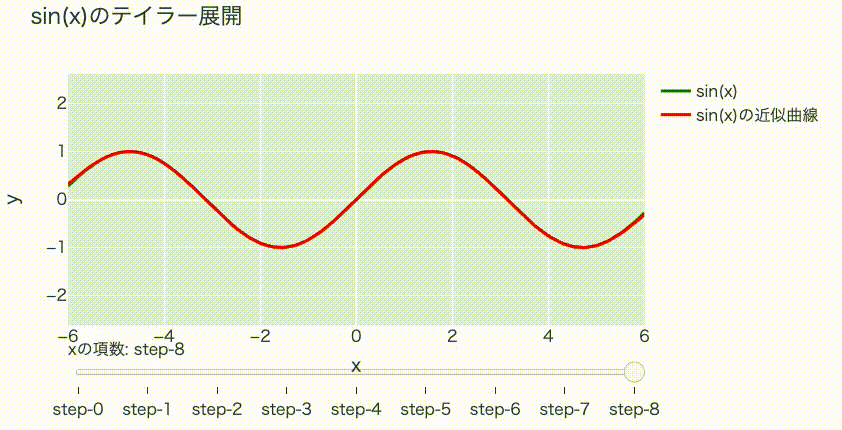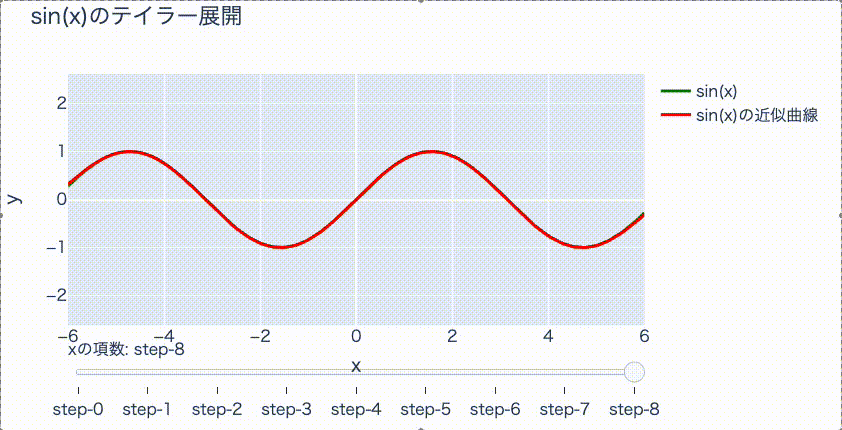
このテイラー展開による近似は、多項式、つまり掛け算と足し算だけで関数を表現できるという特徴があります。そのため、プログラミングにおける数学関係のライブラリでも、\(\sin x\)などの関数を計算するのに使用されています。
前回の記事では関数を近似する方法としてテイラー展開を紹介しました。今回の記事では、同じように関数を近似するフーリエ級数展開について紹介し、身近なところでどのように使われているかについて見ていきたいと思います。
周期的な関数を近似する「フーリエ級数展開」
今回紹介するのはフーリエ級数展開というものです。これもテイラー展開と同じように関数を近似する方法の1つなのですが、テイラー展開とは異なり周期的な関数を\(\sin\)や\(\cos\)で近似するのに使います。
波を重ね合わせる
まず基本的な用語として、「重ね合わせる」という言葉の意味を説明します。例えば\(y=\sin x\)と\(y=\sin 2x\)の関数をグラフにすると次のようになります。
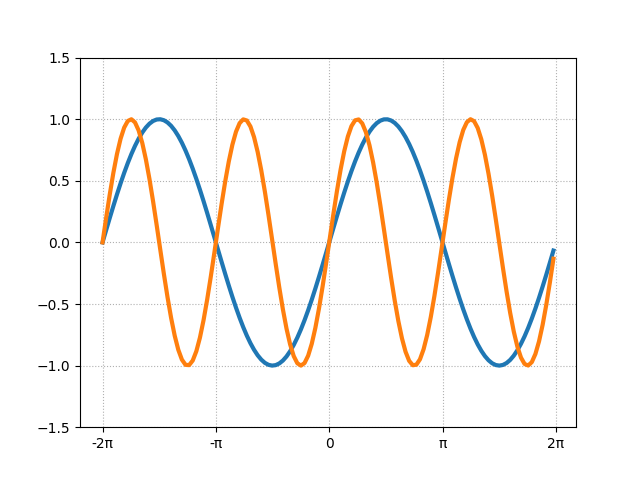
青い線が\(y=\sin x\)で、オレンジの線が\(y=\sin 2x\)のグラフです。周期が異なる2つの波を表しています。周期というのは、繰り返している部分の長さです。この青い線の場合、\(-\pi\)から\(\pi\)までの形を繰り返しているので、周期は\(2\pi\)です。またオレンジの周期はその半分のπです。
この2つのグラフを足し合わせると次のようになります。
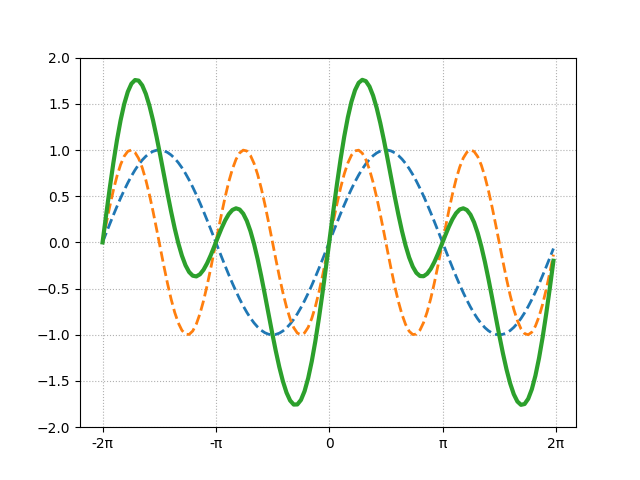
緑の線が2つの波形を足し合わせた結果です。このように、波を足し合わせることを「重ね合わせる」といいます。
フーリエ級数の考え方
先ほどの重ね合わせた結果をよく見ると、波の形は少し複雑になりましたが、同じ形を繰り返していることがわかります。逆に言えば、このように複雑な形であっても、周期的な関数ならば\(\sin\)や\(\cos\)の重ね合わせで表現できるのではないか? というのがフーリエ級数展開の考え方です。
フーリエ級数展開の式は、次のように表現できます。
$$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty} \left( a_n\cos\frac{2nx}{T}+b_n\sin\frac{2nx}{T}\right)$$
ただし、\(a_n\)と\(b_n\)はそれぞれ
$$a_n=\frac{2}{T}\int_{0}^{T}f(x)\cos\frac{2nx}{T}dx, b_n=\frac{2}{T}\int_{0}{T}f(x)\sin\frac{2nx}{T}dx$$
である。
ここで\(T\)は関数\(f(x)\)の周期のことを表しています。\(a\)や\(b\)などの式がごちゃごちゃと書いてありますが、重要なのは、\(\sin\)や\(\cos\)だけで\(f(x)\)が表現されている、つまり、\(\sin\)や\(\cos\)の重ね合わせで表現できるということです。
とはいえ、ここでパッと数式を見せられてもよくわからないと思いますので、もう少し具体的に計算した例を見てみましょう。
矩形波の近似
フーリエ級数展開を学ぶ時、必ず扱うのが矩形波です。矩形波とは、次のようにプラスとマイナスの信号が交互に繰り返す周期的な関数です。
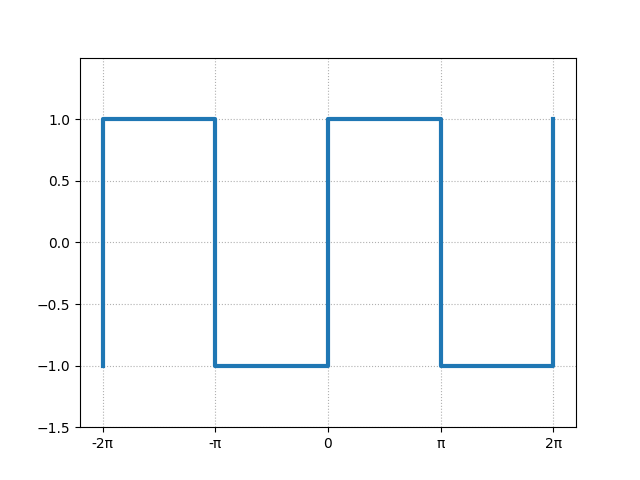
\(n\)を整数として、\(x\)の範囲が\(2n\pi \le x \le (2n+1)\pi\)のときに1、\((2n-1)\pi \le x \le 2n\pi\)のときに-1となります。
これを先ほどのフーリエ級数展開の式に適用して計算すると、こうなります。
$$f(x)=\frac{4}{\pi}\sum_{m=1}^{\infty}\frac{\sin(2m-1)x}{2m-1}=\frac{4}{\pi}\sin x+\frac{4}{3\pi}\sin 3x+\frac{4}{5\pi}\sin 5x+\cdots$$
異なる周期の\(\sin\)関数(\(\sin x\), \(\sin 3x\), \(\sin 5x\), …)を重ね合わせていることがわかります。また\(\frac{4}{\pi}\), \(\frac{4}{3\pi}\), \(\frac{4}{5\pi}\)などの係数は、その周期の重み=強さを表しています。
実際にこれをプロットすると次のようになります。
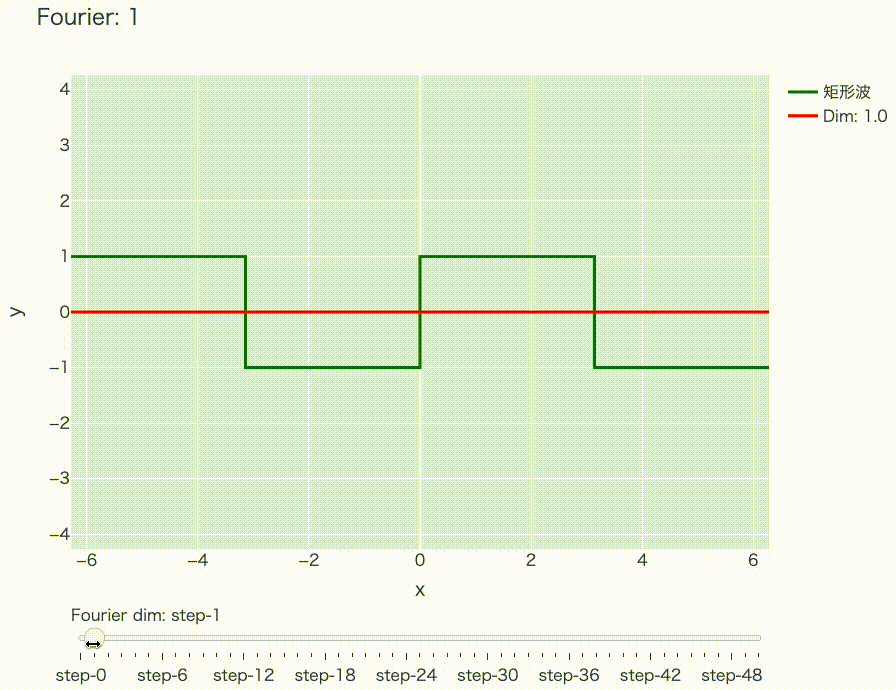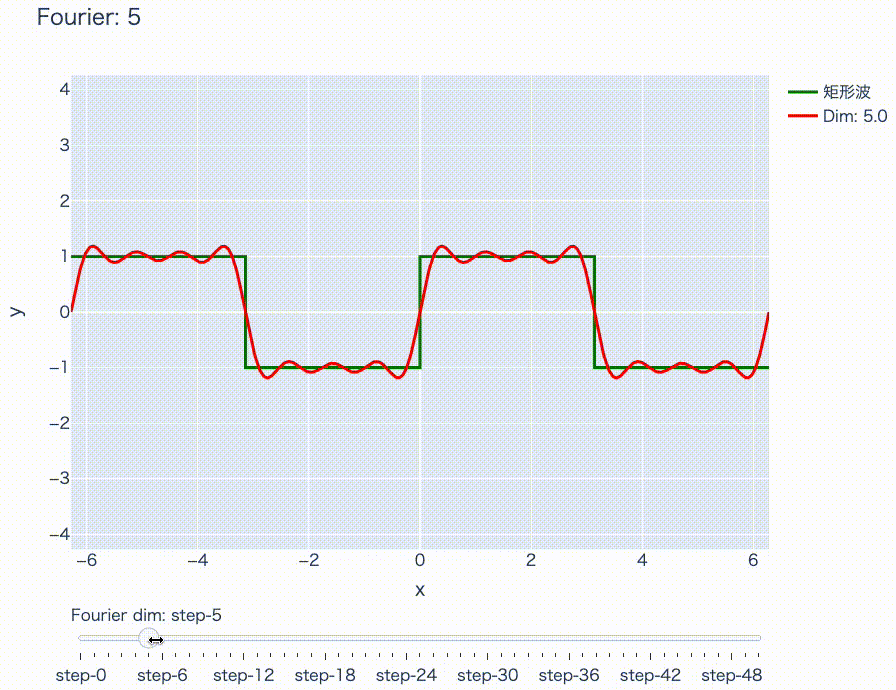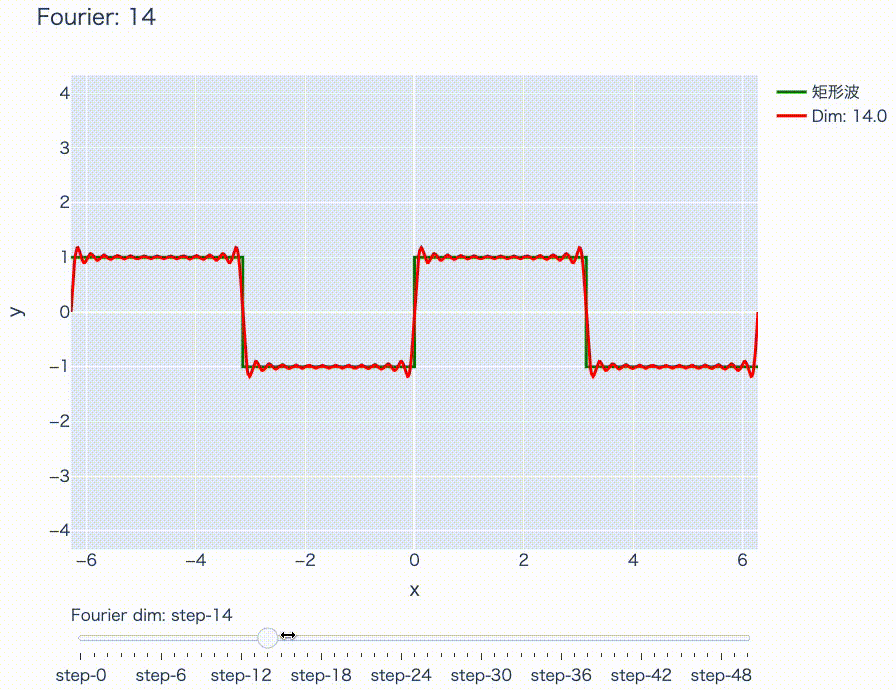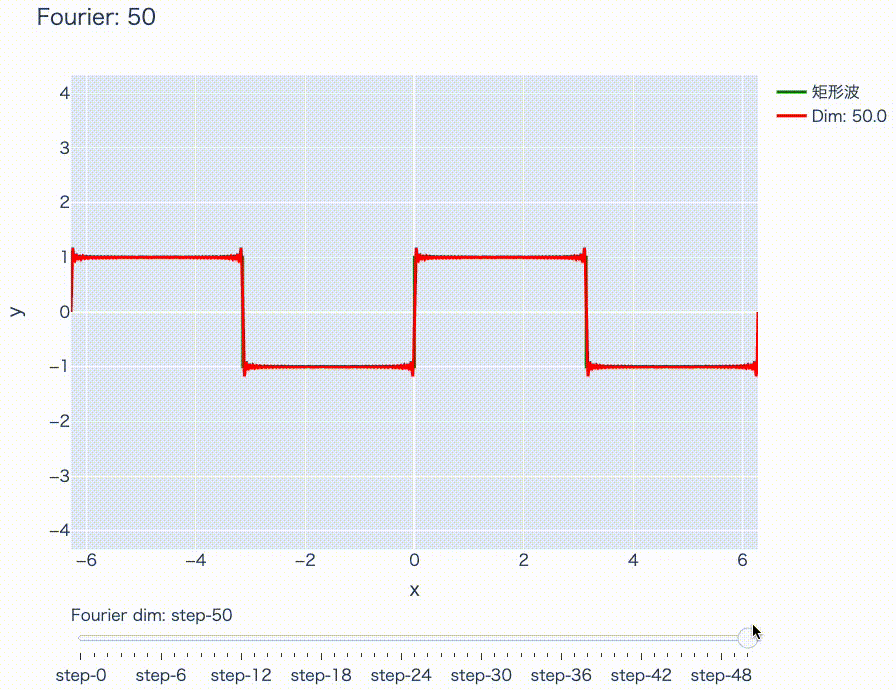
下のスライダーを右にずらすほど、周期の短い\(\sin\)波を重ね合わせています。このようにして、周期的な関数は\(\sin\)や\(\cos\)だけでいい感じに近似できるということが、なんとなくお分かりになったと思います。
関数を構成する波の周期を分析する「フーリエ変換」
フーリエ級数展開を使えば、周期的な関数がsinやcosで近似できることを見ました。これは逆に言えば、周期的な関数がどれぐらいの強さと周期の波の重ね合わせでできているか、ということを調べられるわけです。
ただし、フーリエ級数展開で扱えるのは、周期的な関数だけです。実際に扱いたい関数は必ずしも周期的であるとは限りません。そこで、周期的ではない関数が、どのような波で構成されているかを調べるために考え出されたのがフーリエ変換です。
音波の場合
まずは身近なフーリエ変換の例として「音」について見てみましょう。
次の図は、楽器のチェロの音の波(空気の密度が高くなったり低くなったりする様子)をグラフで表した様子です。
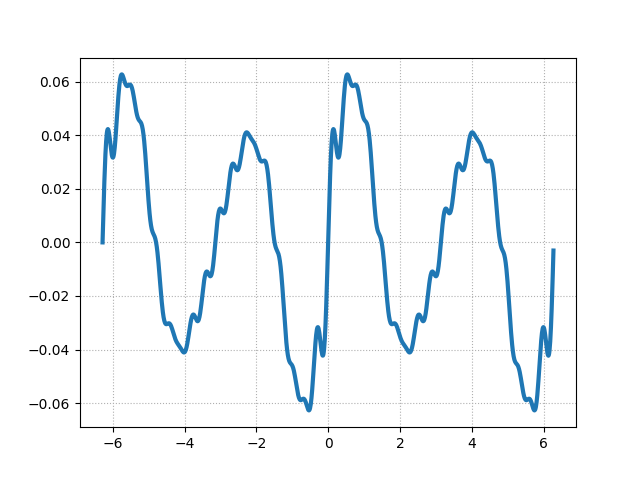
絶対音感を持つ人がこの波形の音を聞くと、「ラの音、しかもチェロの音だ!」と判定することができます。
実は、音を聞いて音階や楽器を当てるというのは、フーリエ変換そのものです。
どういうことか、もう少し詳しく見てみましょう。ドレミの音階とは、音の高低を人間の言葉で表現したものです。実はこの音階はラ(A3)の音を基準にしていて、音波の440Hzという周波数に対応します。440Hzの周波数とは、その波が1秒間あたりに440回振動するということです。
周波数と周期は互いに逆数の関係にあります。周波数が高い、つまり一定の時間の間に振動がたくさん含まれることになるので、その分周期は短くなります。したがって、「その波がどんな周波数の波で構成されているか」と「その波がどんな周期の波で構成されているか」というのは、意味するところは同じです。
さて、「その波がどんな周波数の波で成り立っているか」ということを、次のようなグラフで対応づけてみましょう。440Hzの波でいえば次のようになります。
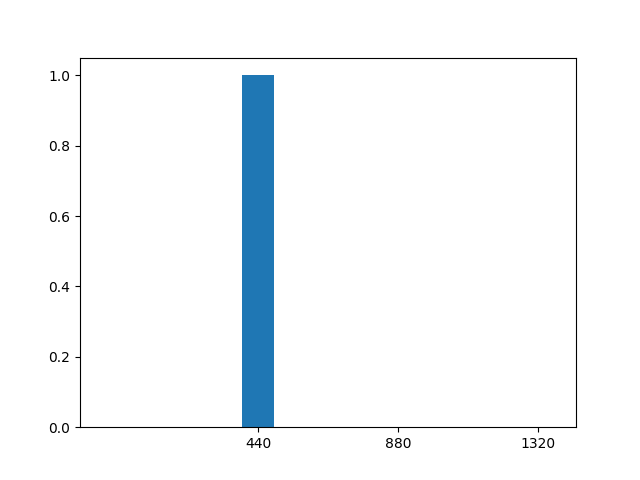
左の画像は音の波形そのものです。この波の周期が440Hzのとき、右のグラフのように440Hzの位置に1本の棒で描きます。棒の高さは、その波の強さ(振幅)に対応します。そして、絶対音感の人が音階を当てることは、この棒の位置を言い当てることに対応します。
さらに、もし880Hzの波がここに混じっていれば880Hzのところにも棒が1本立つことになります。実はこの「異なる周波数の波がどのように混じっているか」が、音色を決めることに当たります。先ほどのチェロの音の波形がどんな周波数で構成されているかをグラフに表すと、次のようになります。
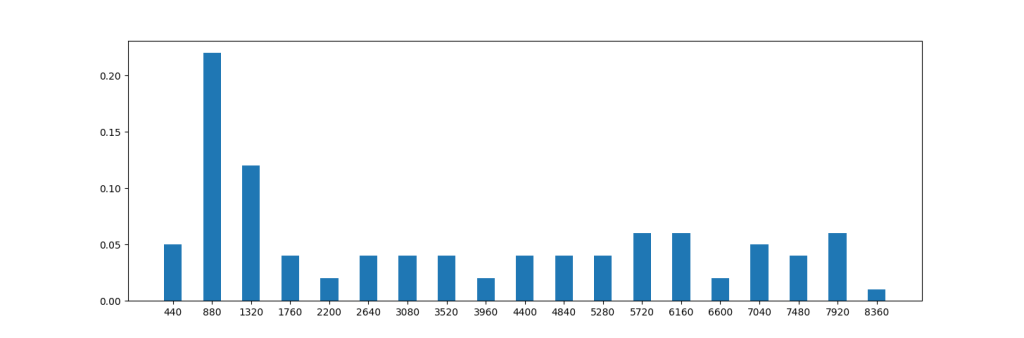
なかなか複雑な構成をしていますね。このような周波数の分布から、この音を出している楽器の種類が判別できます(各周波数の強度はこちらのサイトを参考にしました→https://tomari.org/main/java/audioapi/audio_neiro.html)。
絶対音感のように音の高低をズバリ言い当てられなくても、何の楽器の音かということはわかる人は多いと思います。つまり、人間の耳は音の高低をズバリ当てるよりも、音色、つまりどんな波で構成されているかを聞き分ける方が得意なようです。
周波数の分布を求めるフーリエ変換
先程のチェロの音を構成する周波数のグラフですが、これはあくまで理想的な場合です。実際には先程のグラフのように440Hz、880Hz、…とキリのいい周波数だけでなく、その間にも連続的にさまざまな周波数の波が含まれています。
不正確にはなりますが、イメージとしては、先ほどのグラフの各棒の頂点をこのように結んだ感じです。
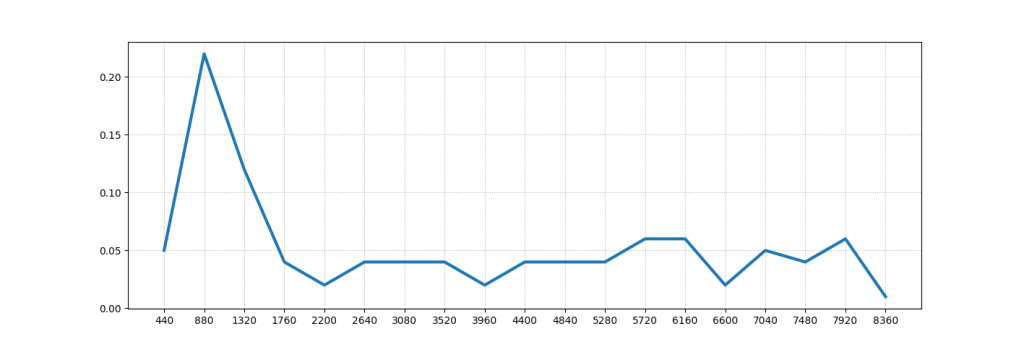
何かしらの信号の関数を\(f(x)\)とすると、このグラフのような周波数\(\tau\)の関数\(F(\tau)\)を求めよう、というのがフーリエ変換です。
この変換を数式で表現したものがこちらです。
$$F(\tau)=\int_{-\infty}^{\infty}f(x)e^{-ix\tau}dx$$
ここでは計算方法は重要ではないので、説明は省略します。
どんな時に使うのか?
ここまで読んで「結局何に使うの?」と疑問に思う方も多いと思います。実は世の中の多くの場面で使われています。
例えば今見てきたような音声の信号の処理では、特定の周波数のノイズを除去したり、データを圧縮したりするのに使われます。
その他にも、物理学や天文学をはじめとする自然科学の分野では、記録した信号にどんな規則性があるかを解析するために使われています。
また身近な例としては、画像をフーリエ変換して不要な周波数成分を除去し、画像サイズを圧縮するのに使われることもあります。
しかし、画像のフーリエ変換と言われても、これはちょっとピンとこないかもしれません。
画像のフーリエ変換
次の画像は、左が入力画像、右がフーリエ変換後の周波数画像です。

右の周波数画像の左右方向がx軸方向の周波数、上下方向がy方向の周波数の波を表しています。そして色が明るいほどその周波数の成分が強いという意味です。
もう少しわかりやすくするために、波を1つだけ表示してみましょう。
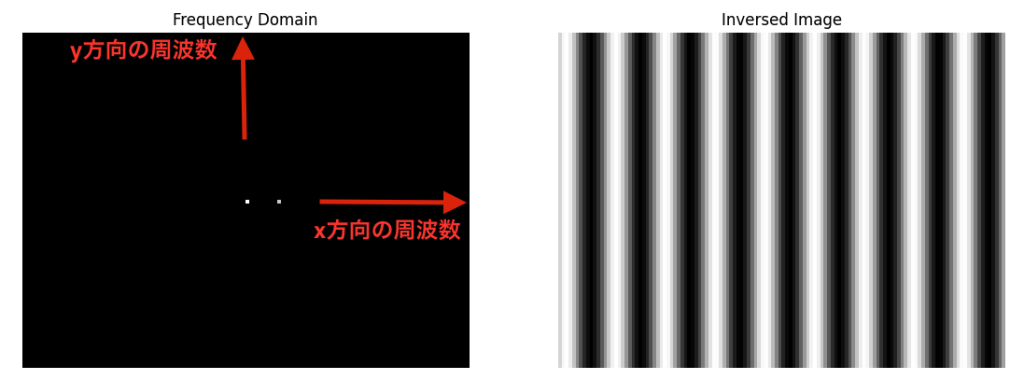
上左の画像は周波数画像で、その中央とその右にもう1つ白い点がありますが、右の点がx方向の波です。上右の画像はその波を画像として表示しています。
いま打った右の白い点より右側は、さらに周波数の高い波に対応します。図で見ると次のようになります。

周波数が高いということは、周期が短いということなので、間隔の狭い波が表示されています。
同様に、中央よりも上に点を打てば、y方向の波になります。

斜め右方向に点を打てば、斜め右方向の波になります。

これを踏まえて先ほどの画像を改めて見ると、意味がわかるのではないでしょうか。つまり、どんな周期と方向を持った波の重ね合わせなのかということを、画像として表示しているのです。

次の3つの画像はそれぞれ、左が入力画像、中央が周波数画像、右が周波数画像をもとに復元した画像です。
このアニメーションでは、中央の周波数の画像をクリックしたとき、その位置の周波数の波を重ね合わせた結果が右の画像になっています。
中央付近をなぞっているうちは怪しい感じですが、重ね合わせる波を増やしていくうちに、元の画像に近くなっていくのがわかると思います。
この理屈を理解した上で、次の画像をみて下さい。

右の画像は、中央の周波数画像のように周辺部分を黒く(0に)した、つまり高い周波数をカットした画像です。ちょっとぼやけていますが、画像の大きな特徴は低周波の部分だけでそれなりに再現できることがわかります。つまり、画像を波で表現するには、低周波の成分が重要であるということです。
JPEG圧縮はこうした画像の特徴を利用して、フーリエ変換した画像の低周波数部分に重きをおくような処理を行い、画像サイズを小さくしているのです(実際にはもう少し複雑なことをしています)。
おわりに
\(\sin\)や\(\cos\)の話から始まり、近似計算、周波数解析まで紹介しました。
音にしても画像にしても、それらを波という形で捉えて分析することで、ノイズ除去や画像の圧縮といった大きなご利益を得ることが出来ることがわかったと思います。
今回紹介した事例以外にも、身近なものにフーリエ変換が使われているものはたくさんあります。興味があればぜひ調べてみてください。

